SatyaCodes

Java- Searching Algorithms

Searching Algorithms

Well, to search an element in a given array, there are two popular algorithms available:

  1. Linear Search

  2. Binary Search


Linear search is a very basic and simple search algorithm. In Linear search, we search an element or value in a given array by traversing the array from the starting, till the desired element or value is found.

For example, consider the following image:

If you want to determine the positions of the occurrence of the number 7 in this array. To determine the positions, every element in the array from start to end, i.e., from index 1 to index 10 will be compared with number 7, to check which element matches the number 7.

Linear Search Algorithim( Array A, Value x)

Step 1: Set i to 1

Step 2: if i > n then go to step 7

Step 3: if A[i] = x then go to step 6

Step 4: Set i to i + 1

Step 5: Go to Step 2

Step 6: Print Element x Found at index i and go to step 8

Step 7: Print element not found

Step 8: Exit

2.Binary Search Algorithm

Binary Search is applied on the sorted array or list of large size. It’s time complexity of O(log n) makes it very fast as compared to other sorting algorithms. The only limitation is that the array or list of elements must be sorted for the binary search algorithm to work on it.

Binary search works only on a sorted set of elements. To use binary search on a collection, the collection must first be sorted.

When binary search is used to perform operations on a sorted set, the number of iterations can always be reduced on the basis of the value that is being searched.

Let us consider the following array:

By using linear search, the position of element 8 will be determined in the 9th iteration.

In BSA, Before we start the search, we need to know the start and end of the range. Let’s call them Low and High.

Low = 0
High = n-1
median = (Low+High)/2;


We need to search for value 3

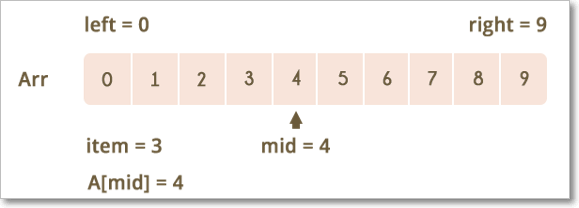
Referring to the image above, the lower bound is 0 and the upper bound is 9. The median of the lower and upper bounds is (lower_bound + upper_bound) / 2 = 4. Here a[4] = 4.

The value 4>2, which is not the value that you are searching for. Therefore, we do not need to conduct a search on any element beyond 4 as the elements beyond it will obviously be greater than 2.

Therefore, we can always drop the upper bound of the array to the position of element 4. Now, we follow the same procedure on the same array with the following values:

Low: 0
High: 3

Repeat this procedure recursively until Low > High. If at any iteration, we get a[mid]=key, we return value of mid. This is the position of key in the array. If key is not present in the array, we return −1.

Search